Utility Function

Utility Function

Under the classic economics assumption of rationality, everyone acts to maximize their “interest.” For any decision-making activity—including investing—if we can measure the “interest” of a decision, we can use optimization methods like calculus to find the best choice.

The concept of utility allows us to quantify the “interest” of a decision. Utility measures the satisfaction or benefit an individual derives from consuming goods and services. The utility function is a mathematical representation of this idea, assigning a numerical value to each possible outcome based on individual preferences.

Example:

\[u(W) = \ln(W)\]

where $W$ is the individual’s wealth. Logically, more wealth leads to higher utility. A rational person should always choose the option that maximizes their expected utility:

\[\text{maximize } E[u(W)]\]

Utility functions are “imaginary” constructs: not only can they take different forms, but each individual may have a different utility function. Utility is a subjective measure of satisfaction and varies from person to person.

Property one: Utility is an increasing function $\implies$ first derivative is positive.

Risk Aversion

Risk aversion describes an individual’s preference for certainty over uncertainty. Consider the following “fair” gamble:

\[\begin{align*} \text{Gamble:} & \quad \text{Win } 100 \text{ with probability } 0.5, \\ & \text{Lose } 100 \text{ with probability } 0.5. \end{align*}\]

A “fair” game means the expected value is zero.

Expressing the gamble as a random variable $\tilde x$ (binomial):

\[\tilde x = \begin{cases} 100 & \text{with probability } 0.5, \\ -100 & \text{with probability } 0.5. \end{cases}\]

In this article, $\tilde x$ denotes a random variable, and $x$ a deterministic value.

Suppose your initial wealth is $W_0 = 1000$. The expected wealth after the gamble is:

\[E[W] = 0.5 \cdot (W_0 + 100) + 0.5 \cdot (W_0 - 100) = W_0\]

If you are unwilling to accept the gamble, you are risk averse. You prefer certainty over the gamble, so:

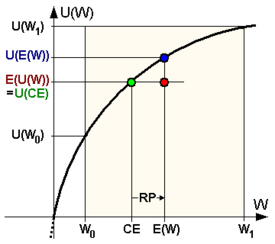
\[u(W_0) > E[\nu(W_0 + \tilde x)]\]

We can quantify risk aversion by how much wealth you are willing to give up to avoid the gamble. The amount you are willing to give up is the risk premium; the remaining wealth is the certainty equivalent:

\[u(W_0) > \nu(W_0 - \pi) = E[\nu(W_0 + \tilde x)]\]

where:

• $\pi$ is the risk premium
• $W_0 - \pi$ is the certainty equivalent

Source: Risk Aversion

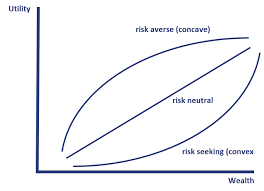
By Jensen’s inequality, a risk-averse person always has a concave utility function.

Source: Certainty Equivalent

Property two: Risk aversion $\implies$ concave utility function $\implies$ second derivative is negative.

Summary

• The utility function is a subjective measure of satisfaction.
• Every individual may have a different utility function.
• Utility functions are increasing: $u’(x) > 0$.
• Risk-averse individuals have concave utility functions: $u’‘(x) < 0$.